Research Area

Counterdiabaticity-assisted ground state preparation for fermionic systems

Objective and Background

Throughout the last couple of years experimental researchers have made great strides in developing larger and better quantum digital computers. Although their advantage in comparison to classical computers has been proven for a select set of problems, there are still many open questions about their utility for physics, chemistry, and other natural sciences. One of the most interesting and practically relevant problems in chemistry is finding the ground states of molecules and we are exploring heuristic methods based on shortcuts to adiabaticity

Many important properties of molecular or condensed matter systems can be inferred from knowing their ground states. However, it has been shown that finding the ground state of a general Hamiltonian is in the QMA-complete class, meaning that it is computationally expensive even with a fault tolerant quantum computer. This necessitates the development and investigation of different heuristic approaches to tackle this problem. Over the last couple of years several methods have been proposed and investigated in detail, most notably the variational quantum eigensolver (VQE) with its different variations and various forms of the unitary coupled cluster Ansatz. 

One of the first proposed methods was the adiabatic state preparation protocol. The general idea is to prepare the quantum register in the ground state of a non-interacting or weakly interacting Hamiltonian, which can be done classically. The register is then subject to a time evolution during which the weakly interacting Hamiltonian is slowly changed into a strongly interacting Hamiltonian. Invoking the adiabatic theorem, the system should stay in the ground state. 

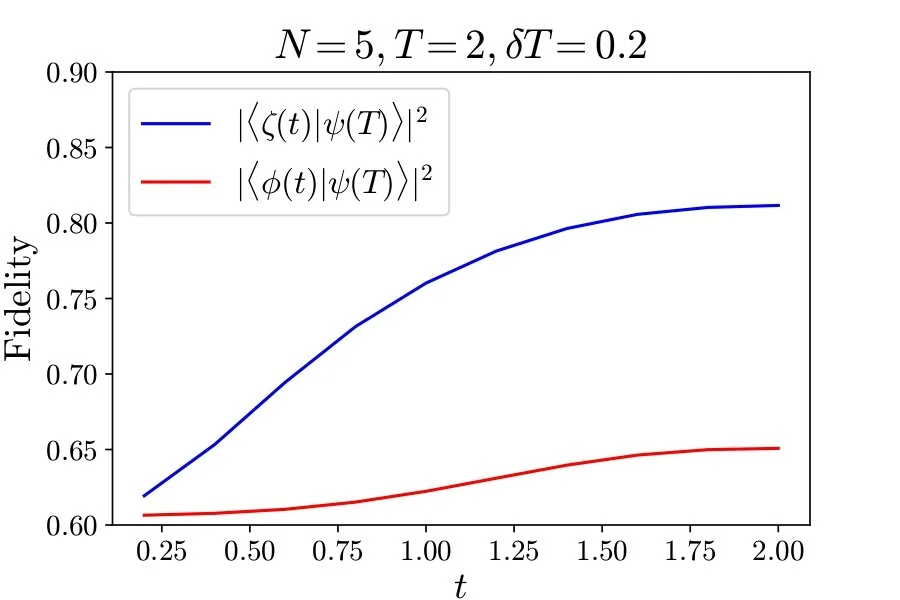
One downside of this method is that it is subject to an error due to a finite evolution time. Recently several methods, termed shortcuts to adiabaticity, have been developed to avoid these in experimental situations. We use one of these approaches, using the nested commutator approximation, in an emulated gate model of quantum computation in order to prepare the ground states of Fermi Hubbard model. We have already demonstrated that the counterdiabatic terms improve the fidelity of prepared ground states, but their implementation comes at a considerable gate cost when compiling via the Suzuki-Trotter decomposition. Currently we are investigating approaches to decrease the gate cost, as well as the applicability of these techniques to molecular Hamiltonians.